
황금비, 저는 인간이 느낄 때 가장 안정적이라고, 아름답다고 느끼는 그러한 두 수의 비율로 그 뜻을 기억했습니다.
황금비 자체의 수학적 정의는 위 사진과 같습니다.
어려운 내용이니 좀 더 풀어서 설명하자면...
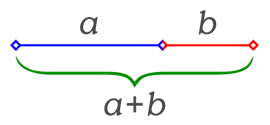
여기서 a+b와 a의 비율이
a와 b사이의 비율과 같을 때
그 비율을 황금비라고 부른다는 겁니다.
우리는 이 비율을 계산해볼 수 있습니다.
수학적 정의에 따르면
여기서 a+b와 a의 비율이
a와 b사이의 비율과 같을 때
라는 조건이 존재하기 때문에, 이것을 그대로 식으로 풀어쓰면 됩니다.
그 전에 비율이라는 것이 무엇이느냐 하면.
두 숫자 사이의 크기가 몇 배 차이이느냐?
라는 개념으로 이해하면 좋습니다.
EX)
1과 2 사이의 크기차이는 두 배입니다.
그래서 '1에 대한 2의 비율'은 2가 됩니다.
또 5와 12 사이의 크기차이는
12/5=2.4이므로 2.4배입니다.
그래서 '5에 대한 12의 비율'은 2.4가 됩니다.
....
그럼 이제 황금비의 정의를 식으로 풀어써보겠습니다.
"a+b와 a의 비율이
a와 b사이의 비율과 같을 때 "
a+b에 대한 a의 비율은
$ a+b/a $가 되고
a에 대한 b의 비율은
$ a/b $가 됩니다.
식의 조건을 살펴보면 그 두 값이 같다고 하였기때문에,
$ a+b/a=a/b $라고 할 수 있습니다.
이 등식 양변에 $ ab $를 곱하여주면,
$ ab+b^2=a^2 $가 됩니다.
양 변을 $ b^2 $으로 나누어줍시다.
$ a/b+1=(a/b)^2 $이 됩니다.
$ a/b $를 한 덩어리로 보아 X라는 문자로 대충 바꾸어 생각합시다.
(보통 치환이라고 표현합니다.)
그렇다면,
$ X^2-X+1=0 $이 됩니다.
이것은 X에 관한 2차방정식입니다.
2차방정식의 근의공식을 적용하여 해 X를 구하면
X값은
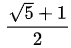
이 됩니다.
이것이 황금비입니다.
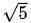
의 값을 잘 계산해서 X값을 다시 계산해주면,
1.61803398....
이라는 값이 나오게 됩니다.
이번 시간에는 수학적 정의를 토대로
그저 그대로 수학적 요소를 계산하는 한 과정을 공부해봤습니다.
구체적으로 이야기하면
1. '비율'이라는 수학적 개념을 이해하고
2. '황금비'의 수학적 정의를 익히고
3. 그것을 토대로 '2차 방정식'을 세우고
4. 그 '2차 방정식'에서 '근의 공식'이라는 수학적 도구를 이요해
5. '황금비'를 계산해내었습니다.
수학은 이렇게
수학적 토대인 정의와 공리에 수학적 사고를 더하여 여러가지 통로를 소풍해나가는 재미가 있습니다.
그리고 그것이 본질에 굉장히 가깝다고도 볼 수 있습니다.
다음 시간에는
이 황금비가 왜 꽤 유명한 수학적 개념으로 대중 사이에 자리잡았는지
그 이유를 살펴보도록 하겠습니다.
'현재와 미래 > 남승우의 수학교실' 카테고리의 다른 글
| 특수함 (3) | 2024.11.13 |
|---|---|
| 정삼각형 숭배 (0) | 2024.11.13 |
| Problem 1 - 미분방정식과 눈덩이의 소멸pt2(end) (0) | 2024.09.21 |
| [번외] 정삼각형의 대칭성 (0) | 2024.09.03 |
| Problem 1 - 미분방정식과 눈덩이의 소멸 pt1 (0) | 2024.08.27 |

