💡 y=X^2을 미분하면 y=2x이다. 그렇다면 왜? 미분이 뭐길래?
1+1이 2임을 친구에게 설명해보자. 저자는 이렇게 설명할 것 같다.
- 1은 무언가 물체가 한 개 있다는 뜻이야. 예를 들어서 네 친구는 한명 뿐이잖아? 그게 1인 거야.
- +라는 기호는 ‘더하기’라고 읽어. 뭔가 추가한다는 의미가 들어간 단어지
- 그럼 1+1의 뜻을 생각해보면 1에 1을 추가한다는 뜻이네?
- 네 친구가 한 명 뿐이었는데, 내가 네 친구가 되어준다면 네 친구는 두명이 되는 것이고
- 따라서 1+1은 2라고 할 수 있겠지
- 1+1이랑 2는 위 설명에 따라서 같은 거니까 1+1=2라고 쓰고
- =이라는 기호는 ‘등호’라고 부르고 ‘같다’라고 읽으면 돼.
얼마나 명쾌한 설명인가?
너무나 상식적이다.
이것이 상식적인 이유는
1+1=2이라는 식에서 어느 한 부분도 직관적으로 또는 논리적으로 설명할 수 없는 것이 없어서이다.
💡 y=X^2을 미분하면 y=2x이다. 친구에게 설명해보자.
1+1=2임을 설명한 것처럼 단어 하나하나의 직관적인 의미를 살펴보면 된다.
- y=x^2은 흔한 ‘이차함수’니까 웬만한 학생들은 알고 있을 것이다. 크게 설명할 소요가 없다.
- ‘미분’이라는 단어는……
????
그야 말대로 ‘????’이다. ‘미분’이 뭔지 설명할 수가 없다. (물론 난 할 수 있다.)
우리는 미분이 뭔지도 모른 채로,
누군가에게 설명할 수도 없는 채로,
미분이라는 수학적 기법을
사용만 해왔다.
“여러분이 어느 회사에 취업했다.
그 회사에서는 당신이 한 단칸방에서 일하게 되는데
그저 의자에 앉아서 1시간마다 책상에 놓인 빨간색 버튼을 눌러주면 된다.
이것이 당신의 일이다.
그럼에도 불구하고 급여는 당연하게도 꼬박꼬박 매달 월급날 입금 된다.”
💡 회사에서 일하고 그에 따른 정당한 대가를 받는다. 사실상 아무런 문제가 없다.
하지만 뭔가 정신이 미쳐갈 것만 같지 않은가?
미분도 똑같다.
여러분은 회사에서 정해진 방식에 따라 업무를 보고 그에 따른 효과로 급여를 받는다.
여러분은 학교에서 정해진 방식에 따라 미분을 하고 그에 따른 효과로 정답을 얻는다.
회사에서의 버튼을 누르는 일이 뭔지도 모른 채 일한다.
수학에서 미분이 뭔지도 모른채 미분을 한다.
알지도 모른 체 그저 돈을 받아내면 절대 발전 가능성이 없을 것이다.
버튼을 누르는 일만 하면서 먹고 살면 대체 어떤 것을 배울 수 있는가?
미분의 원리, 정의, 뜻, 용도 등을 하나도 모르면서
그저 y=x^2을 미분해서 y=2x를 얻는 과정은 어느 문제의 답을 낼 때에는 문제가 없겠지만
크게 보면 그러한 방식은 절대 발전가능성이 없는 방향이고
우리가 추구하는 수학 감수성을 절대로 발전시킬 수 없다.
💡 따라서 우리는 ‘미분’에 대해 제대로 알고자 한다.
“어떤 함수를 미분하여라.”라고 했을 때 대체 미분한다는 게 뭘까?
1. 미분하다 : "어떤 함수의 도함수를 구하다."
그렇다면 ‘도함수’란 무엇인가?
‘도함수’가 무엇인지 설명할 수 있다면
‘미분하다’의 의미를 설명할 수 있을 것이다.
“그렇다면 함수란 무엇인가”라는 질문을 던져도 좋다. 이번 챕터에선 다루지 않겠지만 알 필요는 있다."
2. 도함수 : "함수 f에 대해 x값에 해당하는 미분계수를 x에 대응시키는 함수"
그렇다면 ‘미분계수’란 무엇인가?
- ‘미분계수’가 무엇인지 설명할 수 있다면
- ‘도함수’의 의미를,
- 이어서 ‘미분하다’의 의미를 설명할 수 있을 것이다.
3. 미분계수 :
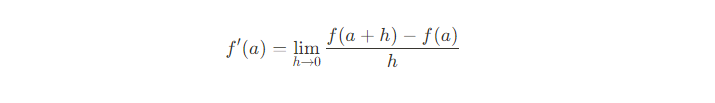
일 때
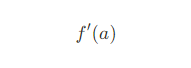
을
함수 f(x)의 x=a에서의 ‘미분계수’라고 정의한다.
참고사항
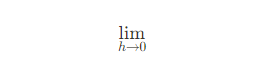
이 식의 의미는 h라는 어떤 수가 존재하여 이 값이 0으로 한없이 가까이 가는 경우를 생각하라는 뜻이다.
‘한없이 가까이’라는 말이 모호하다고 생각이 든다면 자연스러운 것이다.
보통 수학에서는 이렇게 주관적인 단어로 논리를 전개하지 않는다.
2에 한없이 가까운 숫자라고 하면 2.1이라고 해야하는가?
아니면 2.0001이라고, 혹은 1.99라고 해야하는가?
굉장히 모호하다.
이 모호한 내용을 수학적으로 엄밀하게 정의하는 것은 다음에 알아보도록 하자.
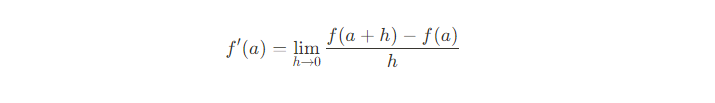
수학적인 개념이 위처럼 정의되면 상당히 모호하기 마련이다.
💡 따라서 예시 하나를 들어보고자 한다.
우리는 ‘미분계수’가 과연 ‘기하학적’으로 무엇을 의미하는지 깨달을 수 있을 것이다.
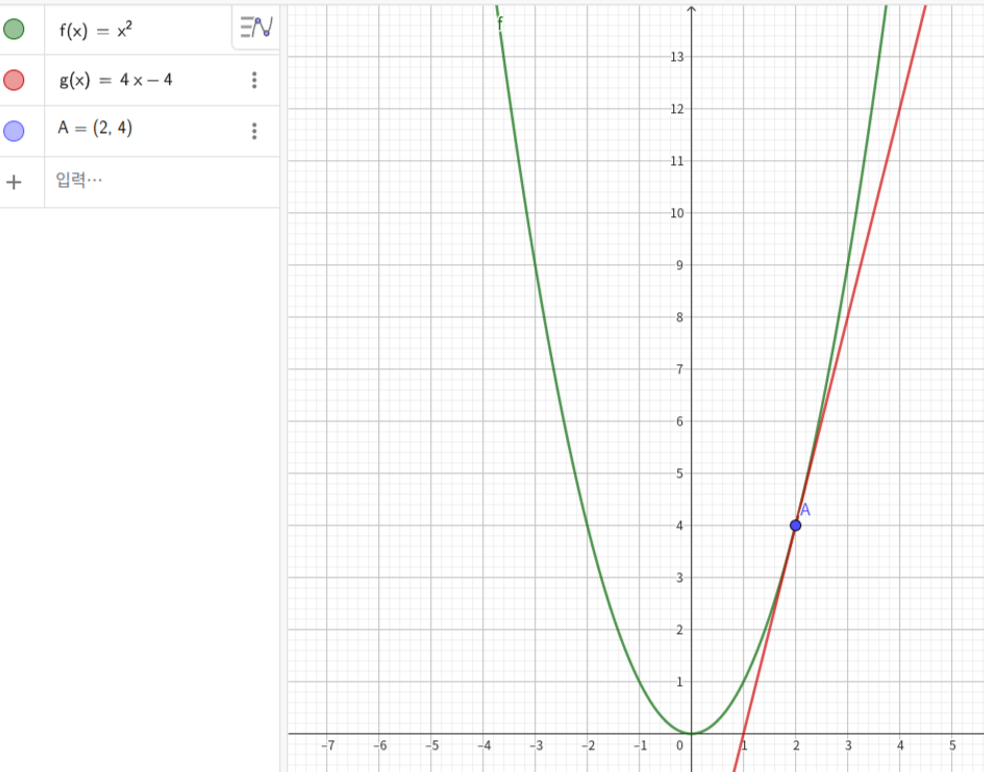
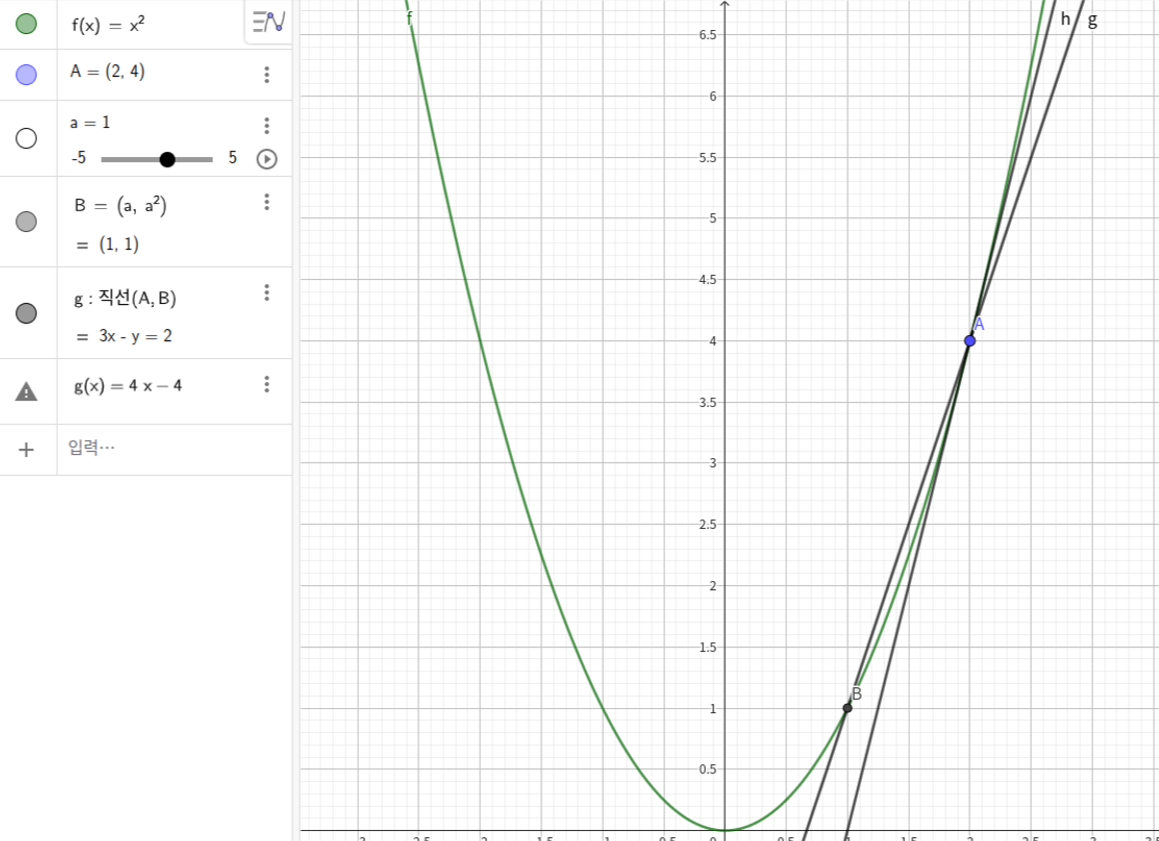
화면 상에 있는 a값 슬라이드 바를 마우스로 마음껏 조작해보자!
(지오지브라에 접속하여 위와 같이 함수를 입력하고 음미해보아라.)
먼저 a가 가장 클 때인 a=4인 경우에서 시작한다.
슬라이드 바를 왼쪽으로 당겨 a의 값을 점점 작게 만들면서 a=2.1인 경우와 a=4의 경우 중
어떤 직선 AB가 더 기존의 접선과 비슷한지 생각해보자.
당연히 a=2.1인 경우일 것이다.
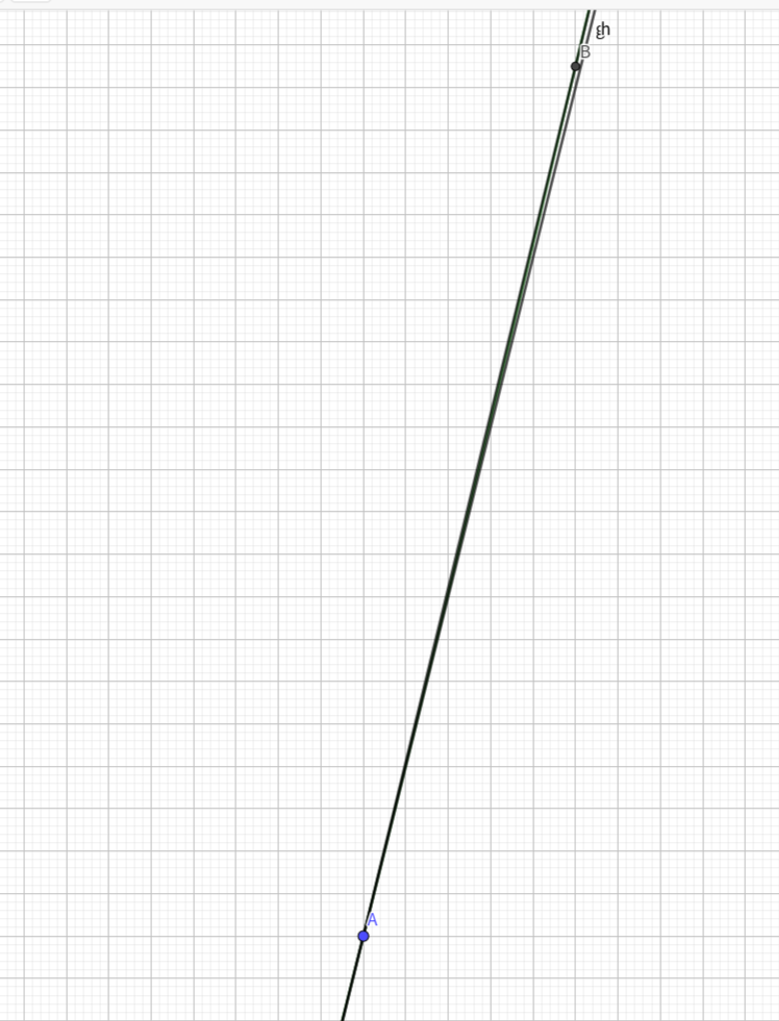
보이듯이 a=2.1인 경우도 화면을 확대해보면 결국 ‘할선’에 불과하지 ‘접선’이 아님을 금방 알 수 있다.
접선은 애초에 함수 f(x)와 g(x)의 그래프 각각이 ‘점 A에서만’ 만나야 하는데
A가 아닌 B를 정의하여 ‘두 개의 점’을 지나는 직선을 ‘접선’이라고 주장하면 말이 안 될 것이다.
하지만 a=2.01이라면 어떻게 될까?
직접 지오지브라에서 a=2.01인 경우를 확인해보자.
a=2.1인 경우보다는 더 접선에 가까운 형태를 지닐 것이다.
솔직히 이정도면 멀리서 보면 '그게 그거지'라는 문과식 마인드를 가질 수도 있을 것이다.
a=2.001인 경우는 a=2.01인 경우보다도 더 접선에 가까운 형태이지만
절대 ‘할선’은 ‘접선’이 될 수 없다.
그럼에도 불구하고 a값이
4에서 2.1
2.1에서 2.01
2.01에서 2.001
.
.
.
2.00000000000000000001에서 2.000000000000000000001
이렇게 ‘한없이 2에 가까워 질수록’
할선 AB는 ‘한없이’ 기존의 접선의 형태로 가까워지는 것은 직관적으로 납득되는 사실이다!
위 사실을 바탕으로 그래프를 살펴보면 할선 AB의 기울기가 점점 접선의 기울기로 가까워지는 것 또한
직관적으로 납득되는 사실이다.
그렇다면 접선의 기울기 대신 그 할선 AB의 기울기를 구해보자.
점 A와 점 B로부터 기울기 m을 구하면
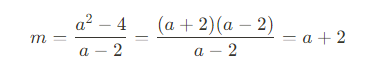
일 것이다.
이 때 a라는 값이 점점 2에 ‘한없이 가까워지는’ 상황을 상상하자.
할선의 기울기는 a+2이니까 우리는
a가 한없이 2로 가까워질때 a+2가 어디로 한없이 가까워지는지가 궁금해야 한다.
다시 말하는데 a+2는 할선의 기울기이고, a가 한없이 2로 가까워지면 할선의 기울기 a+2는 접선의 기울기로 가까워질 것이다.
이 때 할선의 기울기 a+2가 한없이 가까이 다가가는 그 어떤 값을
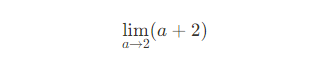
라고 표현한다.
이 값은 곧 할선의 기울기가 한없이 다가가는 값.
할선의 기울기는 접선의 기울기를 향해 한없이 다가가므로
할선의 기울기가 한없이 다가가는 목적지가 곧 접선의 기울기와 같다!
위 식의 의미에 따라서

이런 반복적인 과정을 거치면
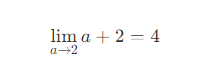
임을 직관적으로 추론할 수 있다.
💡 즉 접선의 기울기는 4가 된다!
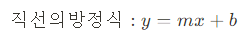
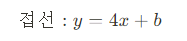
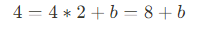
즉,
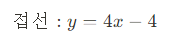
이라는 아름다운 결론에 다다르게 된다!
이 때 숫자 4는 함수 y=x^2의 x=2에서의 미분계수이다.
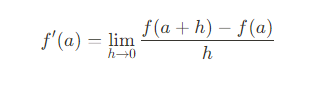
즉, 이 미분계수의 정의에서 f(x)는 x^2을 뜻하는 것이다.
하지만 이것을 살펴보면 h라는 알지 못 할 의미의 상수가 존재한다.
미분계수의 직관적인 의미는 위의 접선을 구하는 과정에서 살펴보았는데,
이것을 h를 이용해 표현한 것이 위의 정의이다.
이것을 다시 기하학적으로 이해해보고자 한다.
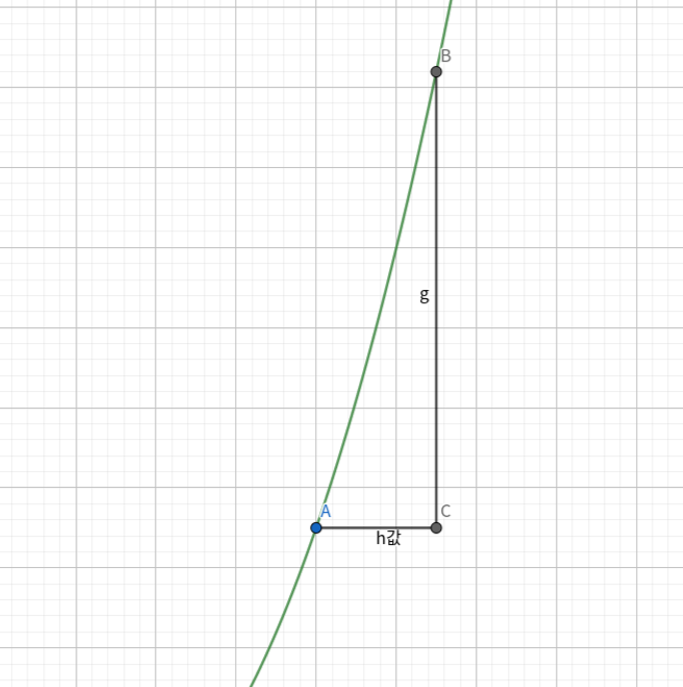
위 이미지에서 초록색 곡선을 y=f(x)라고 정의하자
이 때 A(a,f(a))를 정의하고 x에서 h만큼 떨어져있는 x좌표를 갖는 곡선 y=f(x) 위의 점을 B라고 정의한다.
그렇다면 B(a+h,f(a+h))일 것이다.
이 때 직선 AB의 기울기를 구하면
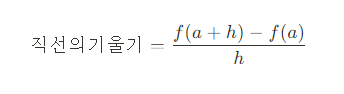
이전에 확인한 접선을 구하는 직관을 이용하여
이번 또한 y=f(x)의 점 A에서의 접선을 구하고자 한다.
이 때 h값을 한없이 0에 가깝게 만들면 직선 AB는 우리가 구하고자 하는 접선에 가까워질 것이다.
즉 위 기울기 값은 h값이 한없이 0에 가까워지면 곧 접선의 기울기값에 가까워진다는 것이다!
이를 다음과 같이 표현한다.
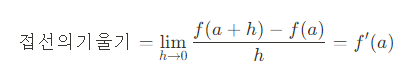
미분계수라 함은 접선의 기울기를 의미한다는 것을 우리는 직관적으로 이해할 수 있다.
이것을 모른 채 아무리 미분을 해서 도함수를 구하고 도함수에 x값을 대입해서 미분계수를 구한다고 하여도
그 미분계수가 사실 접선의 기울기를 의미한다는 사실을 모르면 과연 미분을 제대로 활용할 수 있을까?
사실 미분계수가 접선의 기울기를 의미한다는 것은 쉬운 이야기이지만,
우리가 자세히 살펴본 이 원리들은 굉장히 수학적으로 아름답고 중요한 이야기이다.
위 미분계수의 정의에 의해
a라는 상수에 대해 지점 (a,f(a))에서의 y=f(x)의 접선의 기울기가 곧 그 의미인 것을 이해할 수 있었다.
즉 이러한 미분계수의 논리에 따르면
저 값이 항상 존재하기만 한다면 어떤 a값을 가져다 두어도 항상 f’(a)라는 접선의 기울기를 구할 수 있다는 것이다!
즉, a값이 주어지면 기울기가 주어진다.
이것은 함수이다!
하지만 미분계수의 정의에서 a값은 고정된 상수이기에 이를 일반화하여 x라고 써보자.
즉 y=f(x)라는 함수에서 (x,f(x))에서의 미분계수는 다음과 같다.
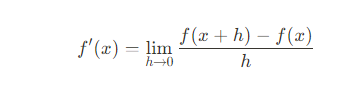
이 식이 의미하는 바는
x값이 어떤 것이 주어져도 우변의 식을 이용해 극한값을 계산하면 좌변의 값인 미분계수,
즉 접선의 기울기를 구할 수 있다는 것이다.
이것은 함수이다!
그리고 이 함수를 ‘도함수’라고 부르자고 약속한다.
즉 ‘도함수’란 미분계수의 일반화 버전이라고 생각하면 된다.
이 때 이 ‘도함수를 구하는 행위 자체’를 “어떤 함수를 미분한다.” 라고 표현하는 것이다.
우리는 이제 ‘미분하다'라는 것이 무엇인지 설명할 수 있다.
미분계수라 함은
어떤 함수의 한 지점에서의 접선의 기울기를 기하학적 직관에 의하여 극한값으로 표현한 것이었고
이를 일반화해 함수로 만들어 쓰는 것을 도함수라고 하고
이 도함수를 구하는 것을 미분이라는 것이다.
누가 어떤 함수를 미분해라. 하면 그 함수의 도함수를 구하면 되는 것이다.
도함수의 정의는 다음과 같았다.
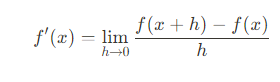
즉, 이 정의를 이용하면 f(x)가 무엇이든 우변의 식을 써서 극한값을 계산해주면 된다는 것이다.
예시로 y=x^2의 x=2에서의 미분계수가 아닌 일반적인 x에 대한 도함수를 계산해보자.
즉 x^2을 미분해보자!
도함수의 정의에 의해 f(x)=x^2일 때 다음이 성립한다.
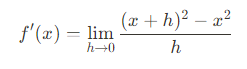
식을 조금만 정리해보면,
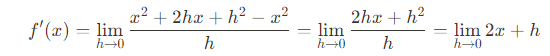
가 된다.
이 때 h가 한없이 0으로 가까이 가는 상황이므로 곧
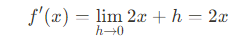
가 된다.
위 식을 그대로 읽어보자.
함수 f(x)의 도함수는 2x입니다.
우리는 y=x^2을 미분하였다!
성공적이다!
비슷한 논리로 여러가지 함수를 모두 미분할 수 있을 것이다.
물론 미분불가능한 함수라는 것이 존재하지만
다음 챕터에서는 y=x^2이 아닌 여러가지 함수의 미분에 대해 배워볼 것이다.
미분이 무엇인지 알기때문에 미분을 유연하게 사용하여 여러가지 생각을 해볼 수 있을 것이다.
숟가락이라는 도구는 밥 먹을 때 식기로 사용할 수 있다.
하지만 숟가락을 이해한 사람은 숟가락은 대부분 딱딱하기 때문에
이를 둔기로 사용할 수도 있다.
즉 숟가락은 사람을 때릴 때 사용할 수 있다.
숟가락은 밥먹을 때 쓴다라고 암기만 했다면
과연 저자는 내가 사준 밥을 먹으면서 불평하는 친구의 이마를 숟가락으로 한 대 치는
혁명적인 제스처를 취할 수 있었을까?
수학 개념은 이해해야 그 쓰임새를 제대로 알 수 있고
유연하게 응용할 수 있게 되는 것이다.
이제 하늘을 우러러 떳떳하게 설명할 수 있다.
아빠 미분이 뭐야?
딸아, 미분은 말이야, 어떠한 함수 y=f(x)에 대하여 x=a에서의 기하학적 근사의 아이디어를 이용해 접선의 기울기를 구하는 극한값을 미분계수라고 정의하는데, 이 미분계수를 x와 대응시켜 만든 함수를 도함수라고 해, 그 때 이 도함수를 구하는 것을 미분이라고 한단다. 그러니까 기울기를 구하는 극한값을 일반화하여 함수를 표현한 것을 미분법을 이용해 구하는 것을 미분이라고 하는 것이지 이해가 정말 잘 되지?
우와! 이해가 너무 잘 되어요!
💡 다시 본론으로!
다음 챕터에서는 여러가지 미분을 도함수의 정의를 이용해 배워볼 것이다.
이를 배우고 나면 웬만한 어떤 함수들을 가져다 두어도 항상 미분할 수 있게 될 것이다.
이러한 방법론인 미분법을 모두 배우고 나면
미분의 활용적인 면을 살펴보고자 한다.
미분의 활용적인 면을 고찰하는 데에 있어서 가장 중요한 것은
사실 미분계수의 기하학적 의미(미분계수는 접선의 기울기를 의미한다.)이다.
굉장히 중요한 내용이라 글이 너무 길어졌습니다.
잘 읽어보고 언제든지 댓글로 태클 혹은 질문 남겨주면 답해드리겠습니다.
전화걸어도 된답니다.
이상
💡 파이팅!
'현재와 미래 > 남승우의 수학교실' 카테고리의 다른 글
| Chapter 5 - 삼각함수의 덧셈정리, 삼각함수의 도함수 (1) | 2024.07.20 |
|---|---|
| Chapter 4 - 곱꼴의 미분법과 유리함수의 도함수 (0) | 2024.07.14 |
| Chapter 3 - 기본적인 미분법과 다항함수의 도함수 (0) | 2024.07.07 |
| Chapter 2 - 여러가지 함수와 미분법 (0) | 2024.07.06 |
| Chapter 0 - 시작하기에 앞서 (0) | 2024.07.06 |



