전 시간에는 함수의 미분에 대해 알아보았다.
미분 다음엔 왜 적분이 아니지? 미적분 아닌가? 하는 의문은 잠시 접어두고
이번 시간엔 여러가지 함수와 그 함수들의 미분법에 대하여 알아보자.
미분법이란 즉 미분하는 방법이니
'미분하다'란 도함수를 구하는 것, 즉 미분법이란
'도함수를 구하는 방법'이다.
도함수를 구하는 방법은 도함수의 정의를 이용하면 되겠다.
1+1의 값이 무엇인지 알기 위해 +의 뜻을 이용하지 않는가?
미분에 있어서 도함수를 구하는 방법은 곧 도함수의 정의를 이용하면 되는 것이다.
본론으로 돌아와서 여러가지 함수에 대해 알아보자.
먼저 함수란 무엇인가?
"1. 어떤 x값을 정해도 항상 그에 대응하는 y값이 존재하며,
2. 모든 x 값 각각에 대응하는 y값이 하나씩만 존재할 때
이 대응관계를 '함수'라고 한다."
예를 들어서
'수학강사 한석원의 x번째 모발 이름'이라는 이름을 가진 대응관계를 지정해보자.

대성 마이맥의 한석원 강사. 그는 탈모로 인해 머리카락이 없다.
시각적인 정보를 이용하니 ★40개쯤★ 되는 것 같다!
그렇다면...
x=1 -> y=1번째 머리카락
x=2 -> y=2번째 머리카락
.
.
.
.
x=40 -> y=40번째 머리카락
x=41 -> 머리카락이 존재하지 않는다!
x=42 -> 머리카락이 존재하지 않는다!
.
.
.
.
x=(40보다 큰 어떤 자연수) -> 머리카락이 존재하지 않는다!
x값이 1부터 40까지는 'x번째 머리카락'이라는 값이 항상 대응되어 존재한다.
하지만 x=41부터는 머리카락이 존재하지 않으므로 41에 대응되는 값이 존재하지 않는 것이다.
하지만 x가 1일 때 부터 40까지의 자연수이면 항상 대응하는 머리카락이 존재한다.
즉 x번째 머리카락이 존재한다.
따라서 x를 1부터 40까지로 제한한다면
1. 어떤 x값을 정해도 그에 대응하는 y값이 존재하고
2. 모든 x값에 대해서 그에 대응하는 y값이 하나씩만 존재하므로
'수학강사 한석원의 x번째 모발 이름'이라는 대응관계는 함수가 맞다.
하지만 x값을 41이상으로 지정한다면
위 대응관계는 함수가 될 수 없다.
왜냐하면 함수의 정의 중 조건 1을 만족하지 않기 때문이다.
이 때 x가 속하는 집합(어떤 값들의 모임이라고 생각하자.)을 '정의역'이라고 하고,
그 정의역의 요소들 각각에 대응되는 y값이 속하는 집합을 '공역'이라고 한다.
위의 함수의 정의는 사실 매우 중요하지만
당분간의 연재 내용에서는 중요 포인트가 되진 않는다. 따라서 가볍게 이해하고 다음으로 넘어가면 되겠다.
이제 여러가지 함수를 알아보자.
(여러가지 함수들에 이름을 붙여 공부할텐데, 그 함수 자체의 정의에 집착하지 마라. 우리가 배울 것에 있어서 큰 의미가 없다.)
1. 다항함수
먼저 가장 흔하게 보는 함수이다.
y=x
이 경우는 우리가 일차함수라고 부른다.
y=2x, y=-3x+40
특히 y=c 꼴의 x 대신 어떤 상수가 있는 경우를 '상수함수'라고 부른다.
다항함수에는 일차함수만 있는 것이 아니다.
y=x^2이나 y=x^3-3x^2+14x-30과 같은 이차, 삼차 함수도 있을 것이다.
즉,
y=a0x^n+a1x^n-1+a2x^n-2+ . . . +an의 형태를 가진 함수를 '다항함수'라고 한다.
2. 유리함수
쉽게 말하면 분수꼴의 함수를 주로 그렇게 부른다.
예를 들어서 y=1/x라던가 y=(x^2+1)/x-1과 같은 분수꼴의 함수이다.
유리함수는 주의해야하는 것이 다항함수처럼 정의역이 자유롭지 못 한다는 것이다.
분수는 분모가 0이 될수 없기때문에 그렇게 만드는 x값을 제외한 실수집합이 주로 그 정의역이 된다.
3. 무리함수
쉽게 말해서 루트가 들어간 함수를 이야기한다.
예를 들어서 y=√x, y=√(x^2-1)와 같은 경우이다.
유리함수처럼 보통 무리함수도 √ 안에 음수가 들어가는 것을 꺼려하기 때문에
정의역이 제한되곤 한다.
4. 삼각함수
삼각함수의 정의는 중요하다!
sinx : 단위원과 x를 나타내는 동경이 만나는 점의 y좌표
cosx : 단위원과 y를 나타내는 동경이 만나는 점의 x좌표
tanx : x를 나타내는 동경의 기울기
cscx : sinx의 역수
secx : cosx의 역수
cotx : tanx의 역수

자세히 알고싶으면
https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=2gumin14&logNo=221133010662
삼각비 2 - 단위원, 그리고 각의 확장
안녕하세요. 지난 포스팅에서는 간략히 삼각비에 대해 설명하고 마쳤습니다. 이번 포스팅부터는 좀 더 깊이...
blog.naver.com
그냥 이런 글 읽으면서 공부해보아라.
글로 설명을 여기에 새로 자세히 하기엔 너무 길다..!
5. 지수함수
지수에 x가 있는 함수이다.
y=2^x와 같은 것이다.
이 때 2를 밑, x를 지수라고 부른다.
6. 로그함수
먼저
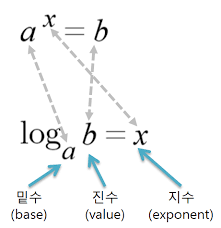
그림에 나오듯 log a b는 말 그대로 '로그 에이 비'라고 읽는다.
이 때 a는 밑수, b는 진수라고 한다.
log의 의미는
밑수가 진수가 되려면 필요한 지수
이다.
예를 들어서
로그 2 4는
밑수인 2가 진수인 4가 되기 위해 2가 필요하기 때문에(2^2=4) 로그값은 2가된다.
또 로그 3 27은 밑수인 3이 진수인 27가 되기 위해 3이 필요하기 때문에(3^3) 로그값은 3이 된다.
즉 로그 a b는 밑수인 a가 진수인 b가 되기 위해 필요한 지수 값을 의미하게 된다.
즉 a^(로그 a b)=b가 된다.
사실 이것이 로그의 정의이다.
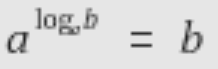
너무나도 당연한 정의이다.
애초에 'log a b가 a라는 수에 지수에 올려두면 b가 되는 수'라는 의미니까 당연히 b가 되어야 한다.
파를 썰면 썰린 파가 생겨야 한다!
이 때 보통 b 대신 x를 넣고 이를 로그함수라고 한다.
즉 y=log 2 x같은 경우이다.
여러가지 함수에 대해 알아보았다.
굉장히 간단하게 설명해서 이해가 안되는 부분도 있을텐데 따로 질문하거나 검색해 공부해보길 바란다.
이제 이 함수들의 미분법에 대해서 알아보자.
기본적인 미분법은 다음과 같다.
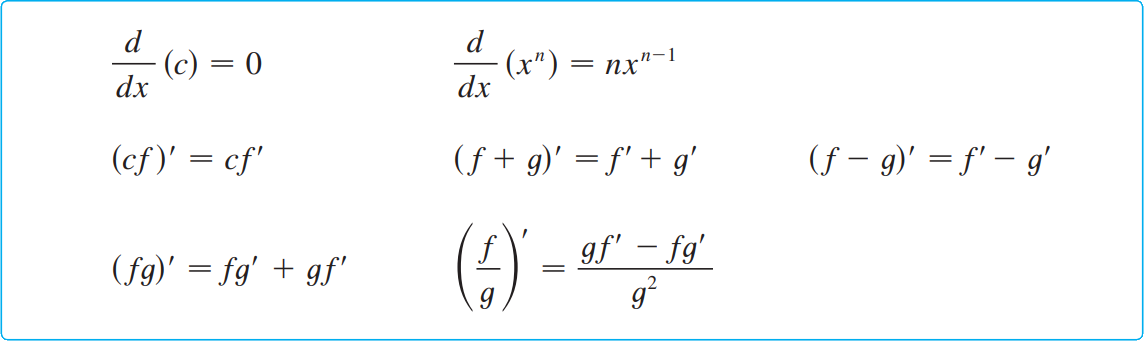
1. 삼각함수의 미분
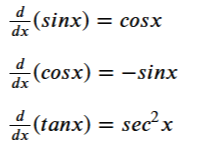
2. 지수함수의 미분
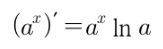
3. 로그함수의 미분
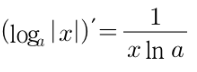
4. 합성함수의 미분
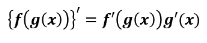
우리는 지금 미분'법'을 배우고 있다.
미분을 하는 방법을 배우는 것이지
이미 미분을 하는 이유는 Chapter 1에서 알아보았다.
그렇다면 미분을 해서 무엇에 어떻게 이용할 수 있을지 알아보는 것은 다음의 이야기일 것이다.
그 다음 이야기로 가기 위해 건너야 할 마지막 관문일 것이다.
바로 다음챕터에서는 각각의 미분법의 증명과 구체적인 활용방법에 대해 배워보자.
이후의 챕터들에서는 본격적인 미분의 적용으로써
선형근사법, 함수의 그래프를 그리는 방법, 뉴턴 방법과 부정적분에 대해 알아보자.
우리는 이들을 거쳐 적분의 개념을 조금 더 배울 것이고
우리의 목적이었던 첫번째 수학적 도구인 미분방정식에 다다르게 된다.
이를 통해 여러가지 현상들을 해석해보고 음미하도록 하자.
이상.
파이팅!
'현재와 미래 > 남승우의 수학교실' 카테고리의 다른 글
| Chapter 5 - 삼각함수의 덧셈정리, 삼각함수의 도함수 (1) | 2024.07.20 |
|---|---|
| Chapter 4 - 곱꼴의 미분법과 유리함수의 도함수 (0) | 2024.07.14 |
| Chapter 3 - 기본적인 미분법과 다항함수의 도함수 (0) | 2024.07.07 |
| Chapter 1 - 미분이란 (2) | 2024.07.06 |
| Chapter 0 - 시작하기에 앞서 (0) | 2024.07.06 |



